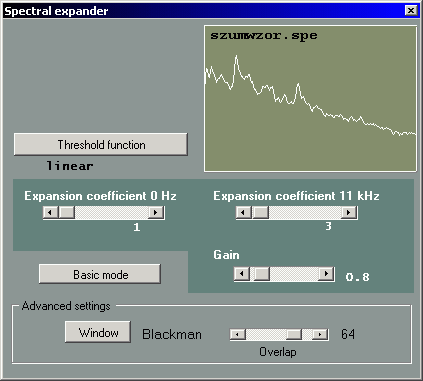
Spectral expander

The spectral expander module enhances the signal intelligibility by increasing the difference between the speech signal level and the level of noise and distortions. It is assumed that the noise is stationary. The algorithm works by comparing the values of observed noise level (in the noisy recordings) and the reference level (in the noise pattern) in a number of frequency bands.

The concept of this algorithm is similar to the spectral subtraction method. The average spectrum of the signal is used to obtain the correction function. Two expansion points that control the shape of correction function may be set by the user: 0 Hz point and the Nyquist frequency point (half the sampling frequency used in the recording). The threshold function has the following form:

where y(n) is the average noise spectrum, N - sample index for Nyquist frequency, a - expansion coefficient for 0 Hz, b - expansion coefficient for Nyquist frequency.

The spectral expansion algorithm is based on the assumption that the speech signal level is much greater than noise level and it is possible to determine the threshold level that will enable noise reduction. Power spectrum of the signal is computed using the FFT algorithm. Spectral components having level above the threshold value are not modified while those below the threshold are processed using the expansion transform:

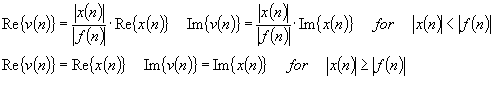
where x(n) is source signal, v(n) - processed signal, f(n) - threshold function.

If the spectral components with level below the threshold were simply removed, this would result in discontinuous spectrum, as in spectral subtraction method. The expansion procedure described above ensures spectrum continuity. If second-order threshold function is used, the dynamic range is doubled (e.g. increase from 6 dB to 12 dB after expansion).

The average noise spectrum is by default computed from the noise pattern file which may be obtained using the spectrum analyser module. The user may set expansion coefficients for low and high frequency range using the sliders (0-100%). Optionally, linear threshold function may be used instead of the noise pattern, by selecting the appropriate option. Expansion coefficient value equal to 0% means no signal modification, larger values mean that more distortions are removed from the signal, but at the same time signal quality may be deteriorated. The choice of expansion coefficients should be a compromise between noise level and speech intelligibility. Additional parameters are: gain (0-1, default value 0.8), time windowing function and amount of overlapping between signal sections in analysis.