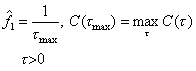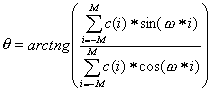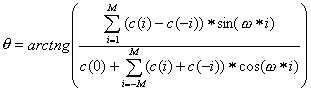Introduction
Zero-Crossing
Autocorrelation Function
CEPSTRUM
Average Magnitude Differential Function
Comb Transformation
FIR Filter Method of Periodic Prediction
Links
Bibliography

---

 

Introduction

Pitch detection is of interest whenever a single quasi­periodic sound source is to be studied or modeled, specifically in speech and music [3][4]. Pitch detection algorithms can be divided into methods which operate in the time domain, frequency domain, or both. 

One group of pitch detection methods uses the detection and timing of some time domain feature. Other time domain methods use autocorrelation functions or difference norms to detect similarity between the waveform and a time lagged version of itself. Another family of methods operates in the frequency domain, locating sinusoidal peaks in the frequency transform of the input signal. 

Other methods use combinations of time and frequency domain techniques to detect pitch. Frequency domain methods call for the signal to be frequency transformed, then the frequency domain rep­ presentation is inspected for the first harmonic, the greatest common divisor of all harmonics, or other such indications of the period. Windowing of the signal is recommended to avoid spectral smearing, and depending on the type of window, a minimum number of periods of the signal must be analyzed to enable accurate location of harmonic peaks [5][6]. Various linear pre­processing steps can be used to make the process of locating frequency domain features easier, such as performing linear prediction on the signal and using the residual signal for pitch detection. Performing non­linear operations such as peak limiting also simplifies the location of harmonics. 

Back

Zero-Crossing

In a time domain feature detection method the signal is usually pre­processed to accentuate some time domain feature, then the time between occurrences of that feature is calculated as the period of the signal [7][8][9]. A typical time domain feature detector is implemented by low pass filtering the signal, then detecting peaks or zero crossings. Linear Predictive Coding (LPC) is often used as a pre­processing step [10]. Since the time between occurrences of a particular feature is used as the period estimate, feature detection schemes usually do not use all of the data available. Selection of a different feature yields a different set of pitch estimates [11]. Since estimates of the period are often defined at the instant when features are detected, the frequency samples yielded are non­uniform in time. To avoid the problem of non­uniform time sampling, a window of fixed size is moved through the signal, and a number of detected periods within each window are averaged to obtain the period estimate. For reliable and smooth estimation, the window must be at least a few periods long. For best accuracy, the signal should be interpolated between samples in order to locate the feature occurrence time as accurately as possible. 

Back

Autocorrelation Function

Related to the time­domain feature detector is the autocorrelation method. The autocorrelation of the signal is first formed: 

and for discrete signals:

The main peak in the autocorrelation function is at the zero­lag location (m = 0). The location of the next peak gives an estimate of the period, and the height gives an indication of the periodicity of the signal. For analog signals this estimate is given by:

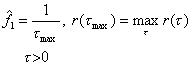
The method usually require a number of periods of data to form a reliable estimate, and thus some averaging of the frequency signal is unavoidable. The method often exhibit difficulty in detecting the period of a periodic signal which is missing the fundamental harmonic in the harmonic series. Periodic but pathological signals can be devised to cause nearly any pitch detection algorithm to fail [12][L3]. 

Back

CEPSTRUM

"Cepstrum" is a play on the word spectrum as one might suspect and is simply a spectrum of a spectrum. The original time signal is transformed using a Fast Fourier Transform (FFT) algorithm and the resulting spectrum is converted to a logarithmic scale. This log scale spectrum is then transformed using the same FFT algorithm to obtain the power cepstrum. The power cepstrum reverts to the time domain and exhibits peaks corresponding to the period of the frequency spacings common in the spectrum:

 

Fundamental frequency is estimated in the same way as in the autocorrelation method:

Back

Average Magnitude Differential Function

The pitch detector/tracker presented here is a refinement of the Average Magnitude Difference Function (AMDF) detectors [14], the earliest of which is that of Miller and Weibel [16]. Methods of this type have also been called comb­filter methods [17]. The AMDF pitch detector forms a function which is the compliment of the autocorrelation function, in that it measures the difference between the waveform and a lagged version of itself. The generalized AMDF function is: 

and fundamental frequency is the smallest period value taken as:

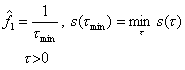
For discrete signals AMDF function is given by:

The quantity k is set to 1 for average magnitude difference, and other values for other related methods. The zero lag (m=0) position of the AMDF function is identically zero, and the next significant null is a likely estimate of the period. Other nulls will occur at integer multiples of the period. The signal is preprocessed to aid in detection of the first null. The difficulties of using this pitch detection method arise from the issues of finite sampling rate, noise, and signal stationarity. If the signal is truly periodic with period T_u, and T_u is an integer multiple of the sampling period T_s , then all nulls at integer multiples of T_u are identically zero. If the period is not an integer multiple of T_s , however, the first null (m<> 0) actually exists between two values of m. A coarse estimate of pitch is tolerable for many speech applications, but is not acceptable for analysis and synthesis of music. Compared to the small computational burden of computing the AMDF, there is no economical method of accurately interpolating between samples to find the true period. This implies that the sampling rate must be sufficiently high to yield the high accuracy required for musical applications. If the signal is quasi­periodic (amplitude modulated, corrupted by noise, etc.), the nulls will never be zero, even if T_u is an integer multiple of T_s . The problem of interpolation between lag samples to obtain an accurate pitch estimate is even further complicated in the case of a frequency modulated signal. 

Back

Comb Transformation

Most of pitch detection methods (e. g. based on autocorrelation function, AMDF) uses only information about frequencies of first peaks in harmonic series. Fundamental frequency, however, can be estimated taking the knowledge about higher frequency peaks. For example, dividing frequency of nth spectral component by n (if signal is harmonic). So, for more accurate estimation of pitch, it may be useful not to get rid of information about higher frequencies.  

One of methods which use this conclusion is cepstrum, described above. If we assume that signal x(t) is harmonic, there is another way to detect its fundamental frequency - comb transformation method [1], which is defined: 

where:

  – comb function,

M –  number of components of comb function,
a_k  – amplitude coefficients of comb function components. In particular case a_k = 1,
w – window function. This function can be chosen, arbitrary, but it must be symmetric (i. g. Gaussian function, triangular etc.).
t – time frame of analyzed signal.

Two important features of comb transformation:

1. different to classical Fourier transformation, where core is one orthogonal base 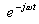, comb transformation has core which is linear combination:

As the effect, core of comb transformation is more correlated with analyzed harmonic signal.

2. comparing to Fourier transformation, where length of window is constant, window used in comb method decrements its size when incrementing parameter k. As a consequence, length of window decreases with increasing of frequency. It betters quality of time-frequency resolution.

 Back

The frequency w  is the frequency at which the phase delay of the filter is calculated. The frequences of interest in calculating the phase delay are the harmonics of the fundamental that it is desired to detect, so some uncertainty is present in the initial calculations. A coarse calculation of w  can be performed by using the value of P, in which case the value of w  is stored and reused as long as the integer value of P does not change. If a more accurate estimate is required, the last predicted period is used to compute w, or the calculation of w  and the pitch estimate is iterated until a desired accuracy is reached. The relation between the pitch estimate and w  is: 

where T_s is the sampling period in seconds and T_u is the period estimate. Computation is reduced by exploiting the evenness and oddness of the cosine and sine functions, and the symmetry of the filter definition. Equation thus reduces to: 

For further computational savings, sine, cosine, and arctng values can be calculated by interpolated table lookup. The phase delay of the filter is computed by: 

By adding the computed time delay to the time delay of the P length delay line, the net time delay of the predictor is computed. This total delay is then used to compute a period and frequency estimate: