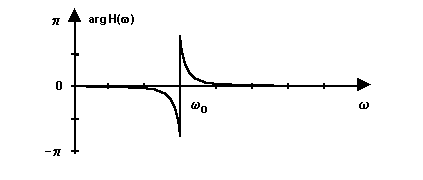Introduction Echo Reverb Flanger Chorus Phaser

---

Introduction

Sound effects as echo, reverb, chorus, flanger or phaser are indispensable in sound productions. They are also part of every-day use equipment.
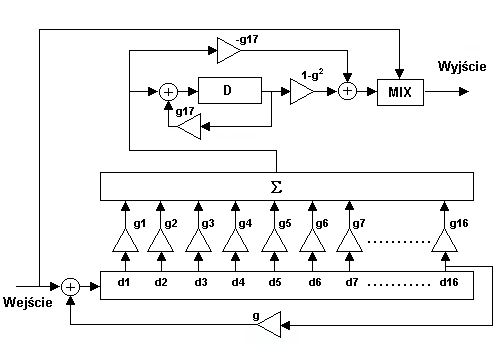
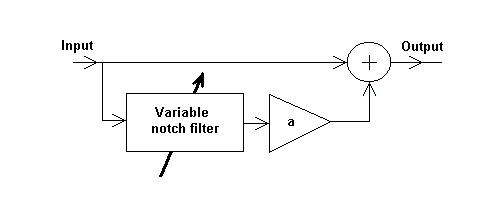
Most of them is realized with a signal processor, which can be as a separate module or on the same board, for example in a keyboard or a synthesizer module. A typical idea scheme is shown on pic.1.

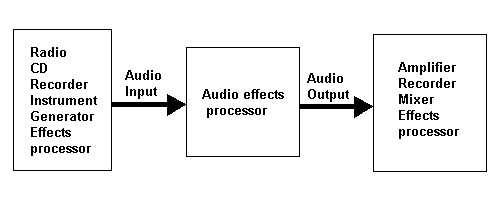
Pic.1. The scheme of sound processing system

The processor takes the input signal from an instrument or a recorder and samples it, for example with a 44.1kHz frequency. Then the signal is processed according to an algorithm, reconstructed to an analog state and put to next system device, for example an acoustic amplifier.
In digital systems the process of sampling and reconstruction can be omitted and the signal is transmitted only in a digitalized state. It is necessary to remember if sample frequencies of particular system elements are the same, and if not a digital signal resample algorithm is needed.

The sound effects have become a part of sythesizers in 80's, when they were improving sounds of piano or strings by use of chorus, and in 90's have become an integral part of such devices.
 

to the top
 

Echo

An echo is a repetition of the original audio sound after a fixed time period with attenuated amplitude. The effect imitates acoustic wave reflections from the large, distant obstacles. If the repetition is fast it is called flattering echo.
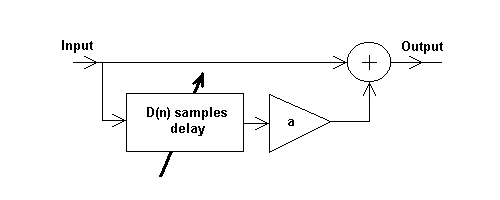
The realization of a single reflection is simple : it is a FIR filter with only one delay line as shown on pic.2.

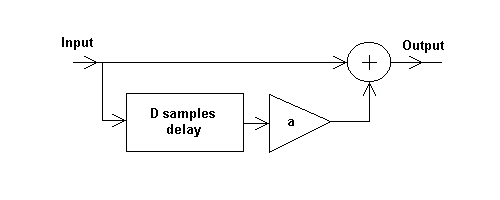
Pic.2. The scheme of FIR filter

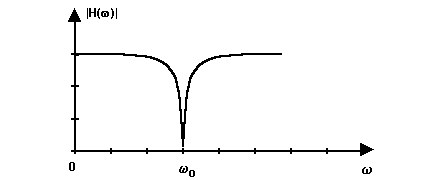
The difference equation is as follows y(n)=x(n)+ax(n-D) , where D is a delay in samples, and coefficient a describes the attenuation related with an object reflection. The transfer function is H(z)=1+az^-D, so the magnitude response has dips at w=2kp/D with magnitude 1-a and peaks at w=(2k-1)p/D with magnitude 1+a.

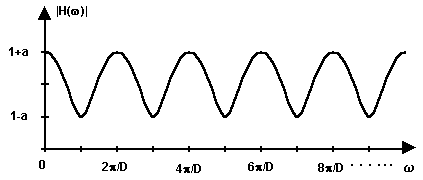
Pic.3. The magnitude of FIR filter

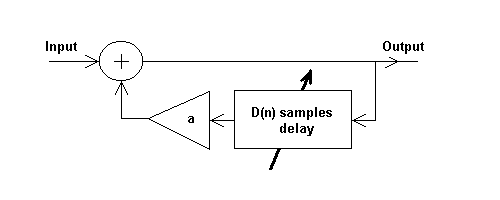
The realization of multiple echo with equal intervals is an IIR filter shown on pic.4.

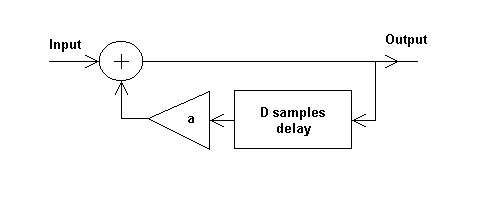
Pic.4. The scheme of IIR filter

The difference equation is as follows y(n)=ay(n-D) +x(n), where D is a delay in samples, and coefficient a describes the attenuation related with an object reflection. As the transfer function is H(z)=1/(1-az^-D) , so the magnitude response has dips at w=(2k-1)p/D with magnitude 1/(1+a) and peaks at w=2kp/D with magnitude 1/(1-a). One should remember that IIR filter can be unstable, so a<1. Otherwise the filter becomes a generator.

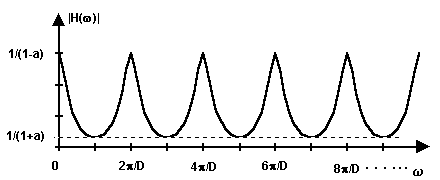
Pic.5. The magnitude of IIR filter

Of course, to get the echo effect the delay should be significant D = [td*fs], where td>100ms, therefore at sample frequency fs=44,1kHz the delay is D>4410. You can get a comb filter if time delay td is about milliseconds. The effect can also be modified by replacing scaling element a lowpass filter, it simulates stronger attenuation of high frequencies than low frequencies.

In synthesizers the echo can be obtained by retriggering ADSR envelope generator or generating again MIDI code.
 

Sound examples

	The echo applied to a clean guitar (2*103kB)
	The echo applied to a distorted guitar (2*110kB)
	The comb filter applied to a distorted guitar (2*38kB)
	The echo applied to a percussion appropriately (146kB+170kB)
	The echo applied to a percussion inappropriately (260kB)

to the top
 

Reverb

The reverberation phenomenon is present in every limited space and is the result of complex acoustic wave reflections from walls as well as other objects. The amount of these reflections is so high that they are unperceived by human ear. To state the quantity of reverberation it is necessary to measure reverberation time defined as the time after which the energy of reflected acoustical wave decreases to level of -60dB in relation to the level in the moment of switching off the test impulse.
The phenomenon has two phases :
1. early reflections - waves reflected for the first time reach the listener
2. reverberation - reiteratedly reflected waves that are unperceived

The early realizations were based on mechanical interference - a spring-line reverberation unit, used till now in guitar amplifiers - and tape-based feedback flutter echo unit. Next development step was analog delay line replaced in 80's by its digital version, and then signal processors have been applied, so every parameter can be simulated.
The reverb is very important in acoustics. The reverberation quality influence on speech intelligibility and instrument sound. Thanks to the artificial reverb it is possible to regulate the spaciousness of recordings and other sound productions.
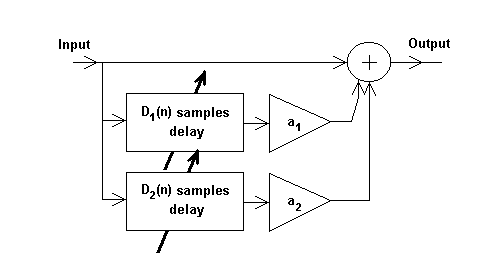
The reverb algorithm is consisted of a few filters mentioned in echo chapter, but this time the time delays are much shorter. There is also new type of filter - allpass filter. The filter gives the same effect as echo, but the magnitude response in constant in frequency domain - so the coloration effect is omitted.

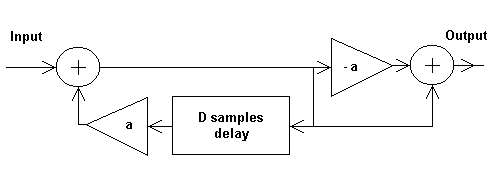
Pic.6. The allpass filter

The transfer function is H(z)=(-a+z^-D)/(1-az^-D).
Because the reverb algorithm is much sophisticated there is plenty of solutions. The algorithm below is Schroeder algorithm.

Pic.7. The scheme of Schroeder reverb

The flanger is a kind of comb filter which delay D is not constant, but changes periodically.

Pic.8. The scheme of FIR flanger

The difference equation is y(n)=x(n)+ax(n-D(n)), where, for example D(n)=d/2(1-cos(2pFn)), F - deviation speed (about 1 Hz), d - deviation rate.
The modulation of delay time causes dynamic changes in dips and peaks position. Additional effect is time stretching of audio signal. The time delay varies between 1 and 5 ms. Alike echo there is FIR and IIR version.

Pic.9. The scheme of IIR flanger

An analog devices of flanger are based on analog delay line and time delay variation are gained by changes of sampling frequency.
It is necessary to use rounding, truncation or interpolation algorithm to digital effect because of need to calculate the samples at non-integer delay.

Sound examples

	The flanger applied to a clean guitar (2*103kB)
	The flanger applied to a distorted guitar (2*38kB)
	The flanger applied to a percussion (2*103kB)

to the top
 

A chorus effect imitates a group of musicians (singers) playing the same sound (unison). Because musicians are more or less synchronized to reach the effect small delays are used. The changes of delay are random, so the sound is more natural. D(n)=d(0.5+v(n))  or D(n)=d1+(d2-d1)(0.5+v(n)), where v(n)- zero-mean low-frequency random function.

Pic.10. The scheme of chorus imitating three musician play

The analog versions of the chorus are the FIR flanger with delay time varying from 10 o 30ms.

Sound examples

	The chorus applied to a clean guitar (2*103kB)
	The chorus applied to a distorted guitar (2*38kB)
	The chorus applied to a percussion (2*103kB)

to the top
 

The phaser effect is popular among guitarists and keyboardist. The algorithm is based on a phase shifter realized by notch filtering at w_o and the notch frequency varies in time.

Pic.11. The scheme of phaser

At the notch there is a strong phase shift that causes cancellation or enhancement of signals about w_o after adding together. The changes of location at frequency axis is controlled by a low-frequency oscillator or a foot control.

Pic.12. The magnitude of notch

The filter can be calculated in traditional way or an allpass filter cascade can be applied. The phase shift should be about 180^o at particular frequency. The a parameter is responsible for effect intensity.

Pic.13. The phase of notch

Similarly to the flanger a multi-notch filter can be used, but the difference is that notches are irregular.
The analog phasers are still being produced.

The wah-wah effect is based on the same rule, but instead of notch a narrow bandpass filter is used.

Sound examples

	The phaser applied to a clean guitar (2*103kB)
	The phaser applied to a distorted guitar (2*38kB)
	The phaser applied to a percussion (2*103kB)

to the top
 
author: Adam Michalski